RELATED WEBSITE: Emeagwali's Website

Petroleum engineers use the flow pattern within a reservoir to decide where to drill a well, how many wells should be drilled, how to maximize the production from a group of wells, and how and where to apply enhanced oil recovery techniques. An example of a complex reservoir simulator is the Multiple Application Reservoir Simulator (MARS) code developed by Exxon Production Research Company and described in reference. 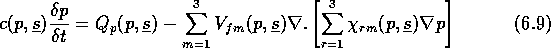Some of the governing partial differential equations used in the MARS code are the pressure equation and saturation equations respectively, where, In the above equations used in the MARS reservoir simulator, the pressure distribution, p(x,y,z,t), in the pressure equation is differentiated to obtain the total fluid velocity distribution which, in turn, is used in the saturation equations. The few instances in which it is not require to differentiate the pressure distribution is when certain least squares or Galerkin finite element approximations of the parabolic equations are used. Unfortunately, existing production codes are based on finite difference techniques. Since the development of these codes are based on decades of man-years the best approach is to use the Fillunger-Risenkampf's since it allows the modeler to reuse the existing codes by reencapsulating the new equations. However, with the new porous media flow governing equations proposed in this work, it will not be necessary to compute the velocity distribution since it will be explicitly available from the solution of the governing equations. Second, Dirichlet type boundary conditions are more accurate than Neumann type in the vicinity of injection and production wells. Third, the governing equations will still be valid when the Reynold's number is high near the injection and production wells. The governing equations for this oil drilling site will be those representing the governing laws for oil, gas, and water. Factors that increase the computation-intensiveness of reservoir simulators include accounting for the thermodynamic and chemical relationships for water, hydrocarbon liquid and hydrocarbon gas phases and accounting for the mass transfer between the liquid and gaseous phases, which occurs from carbon dioxide injection and volatile oil. For example, an IMPES black-oil simulator has five computation-intensive segments. The first and largest portion solves the linear systems of equations approximating the governing equations. Solving these equations consumes 35 to 50 percent of the total execution time. The second segment generates the coefficients and consumes 30 to 40 percent of the total execution time. The third looks up a table to determine the relationship between two functions such as water saturation 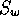and the water relative permeability . 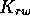These relationships are expressed in tabular form for finite values. Therefore, the exact relationship needed must be determined by interpolation. Table look-up operations consume 15 to 25 percent of the total execution time. Finally, the initialization and input/output operations consume about 10 percent and 2 percent, respectively, of the total execution time. An interesting observation is that by using the proposed complete hyperbolic equations in the reservoir simulator we make the most computation-intensive segment of the simulator to become the least computation-intensive segment which is both good and bad news. Click on emeagwali.com for more information. ©1997. EMEAGWALI.com. All rights reserved.