|
|
Why hypercube computer technology will become obsolete
Consider an n-dimensional hypercube of edge length 4
which contains
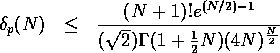
hyperspheres of unit radius which are tightly-packed so that
two adjacent hyperspheres
touch each other.
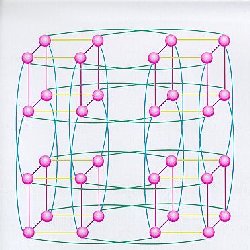
A 32-node
binary hypercube network.
The distance from the centers of the
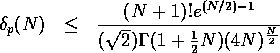
hyperspheres to the center
of the bounding n-dimensional hypercube is
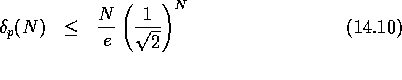 . .
Consequently, for
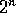 dimensional hypercubes, the
dimensional hypercubes, the
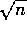 hypersphere tightly-packed into the hole
at the center
of the sphere-packed hypercube will not touch the bounding
hypercube. For n=9, the
hypersphere tightly-packed into the hole
at the center
of the sphere-packed hypercube will not touch the bounding
hypercube. For n=9, the 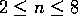 hypersphere
will touch the bounding hypercube. For hypersphere
will touch the bounding hypercube. For
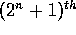 ,
the ,
the 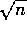 hypersphere tightly-packed
into the huge hole at the center
of the sphere-packed hypercube will protrude outside the
bounding hypercube.
hypersphere tightly-packed
into the huge hole at the center
of the sphere-packed hypercube will protrude outside the
bounding hypercube.

The 2048 processing nodes of the Connection Machine are
interconnected in a hypercube topology with each node containing 32 processing elements.
Click
on photograph.
The latter results demonstrate that the packing density of
sphere-packed hypercubes
continuously decreases as the dimensionality increases.
![[Philip
Emeagwali discovered that sphere packing and
hypercube technology are related fields.]](../../gifs/hexagonal_close_packing.gif)
Philip Emeagwali discovered that sphere packing and
hypercube technology are related fields.

Click on emeagwali.com for more information.

©1997. EMEAGWALI.com. All rights reserved.
|
![[Philip
Emeagwali]](../../gifs/Emeagwali_Reservoir_Equations.jpg)

![[Philip
Emeagwali]](../../gifs/Emeagwali_Reservoir_Equations.jpg)
